ELEMENTS
by Euclid
Translated by Thomas L. Heath
Book One
DEFINITIONS A point is that which has no part.
A line is breadthless length.
The extremities of a line are points.
A straight line is a line which lies evenly with the points on itself.
A surface is that which has length and breadth only.
The extremities of a surface are lines.
A plane surface is a surface which lies evenly with the straight lines on itself.
A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.
And when the lines containing the angle are straight, the angle is called rectilineal.
When a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.
An obtuse angle is an angle greater than a right angle.
An acute angle is an angle less than a right angle.
A boundary is that which is an extremity of anything.
A figure is that which is contained by any boundary or boundaries.
A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another;
And the point is called the centre of the circle.
A diameter of the circle is any straight line drawn through the centre and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle.
A semicircle is the figure contained by the diameter and the circumference cut off by it. And the centre of the semicircle is the same as that of the circle.
Rectilineal figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than four straight lines.
Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle that which has two of its sides alone equal, and a scalene triangle that which has its three sides unequal.
Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acuteangled triangle that which has its three angles acute.
Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia.
Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.
POSTULATES
Let the following be postulated:
To draw a straight line from any point to any point.
To produce a finite straight line continuously in a straight line.
To describe a circle with any centre and distance.
That all right angles are equal to one another.
That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
COMMON NOTIONS
Things which are equal to the same thing are also equal to one another.
If equals be added to equals, the wholes are equal.
If equals be subtracted from equals, the remainders are equal.
[7] Things which coincide with one another are equal to one another.
[8] The whole is greater than the part.
PROPOSITIONS
Proposition 1
On a given finite straight line to construct an equilateral triangle.
Let AB be the given finite straight line.
Thus it is required to construct an equilateral triangle on the straight line AB.
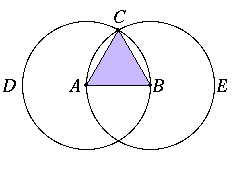
With centre A and distance AB let the circle BCD be described; [Post. 3]
again, with centre B and distance BA let the circle ACE be described; [Post. 3] and from the point C, in which the circles cut one another, to the points A, B let the straight lines CA, CB be joined. [Post. 1]
Now, since the point A is the centre of the circle CDB,
AC is equal to AB. [Def. 15]Again, since the point B is the centre of the circle CAE,
BC is equal to BA. [Def. 15]But CA was also proved equal to AB;
therefore each of the straight lines CA, CB is equal to AB.
And things which are equal to the same thing are also equal to one another; [C.N. 1]
therefore CA is also equal to CB.Therefore the three straight lines CA, AB, BC are equal to one another.
Therefore the triangle ABC is equilateral; and it has been constructed on the given finite straight line AB.
(Being) what it was required to do.
1. On a given finite straight line. 3. Let AB be the given finite straight line. 8. let the circle BCD be described. 13. from the point C.... 20. each of the straight lines CA, CBProposition 2.
To place at a given point (as an extremity) a straight line equal to a given straight line.
Let A be the given point, and BC the given straight line.
Thus it is required to place at the point A (as an extremity)
a straight line equal to the given straight line BC.
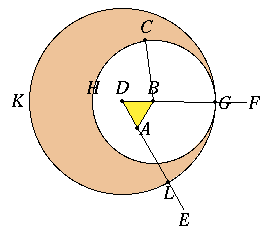
From the point A to the point B let the straight line AB be joined; [Post. 1] and on it let the equilateral triangle
DAB be constructed. [I. 1]
Let the straight lines AE, BF be produced in a straight line with DA, DB; [Post. 2] with centre B and distance BC let the
circle CGH be described; [Post. 3] and again, with centre D and distance DG let the circle GKL be described. [Post. 3]
Then, since the point B is the centre of the circle CGH,
BC is equal to BG.Again, since the point D is the centre of the circle GKL,
DL is equal to DG.And in these DA is equal to DB;
therefore the remainder AL is equal to the remainder BG. [C.N. 3]But BC was also proved equal to BG;
therefore each of the straight lines AL, BC is equal to BG.And things which are equal to the same thing are also equal to one another; [C.N. 1]
therefore AL is also equal to BC.
Therefore at the given point A the straight line AL is placed equal to the given straight line BC.
(Being) what it was required to do.
1. (as an extremity). 11. Let the straight lines AE, BF be produced.... 23. the remainder AL...the remainder BG.Proposition 3.
Given two unequal straight lines, to cut off from the greater a straight line equal to the less.
[Figure]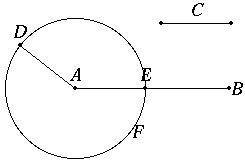
Let AB, C be the-two given unequal straight lines, and let AB be the greater of them.
Thus it is required to cut off from AB the greater a straight line equal to C the less.
At the point A let AD be placed equal to the straight line C; [I. 2] and with centre A and distance AD let the circle DEF be described. [Post. 3]
Now, since the point A is the centre of the circle DEF, AE is equal to AD. [Def. 15] But C is also equal to AD. Therefore each of the straight lines AE, C is equal to AD; so that AE is also equal to C. [C.N. 1]Therefore, given the two straight lines AB, C, from AB the greater AE has been cut off equal to C the less.
(Being) what it was required to do.
Proposition 4.
If two triangles have the two sides equal to two sides respectively, and have the angles contained by the equal straight lines equal, they will also have the base equal to the base, the triangle will be equal to the triangle, and the remaining angles
will be equal to the remaining angles respectively, namely those which the equal sides subtend.
Let ABC, DEF be two triangles having the two sides AB, AC equal to the two sides DE, DF respectively, namely AB to DE and AC to DF, and the angle BAC equal to the
angle EDF.
I say that the base BC is also equal to the base EF, the triangle ABC will be equal to the triangle DEF, and the remaining angles will be equal to the remaining angles respectively, namely those which the equal sides subtend, that
is, the angle ABC to the angle DEF, and the angle ACB to the angle DFE.
For, if the triangle ABC be applied to the triangle DEF,
and if the point A be placedon the point D and the straight line AB on DE,
then the point B will also coincide with E, because AB is equal to DE.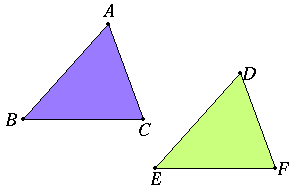
Again, AB coinciding with DE, the straight line AC will also coincide with DF, because the angle BAC is equal to the angle EDF;
hence the point C will also coincide with the point F, because AC is again equal to DF.But B also coincided with E; hence the base BC will coincide with the base EF.
[For if, when B coincides with E and C with F, the base BC does not coincide with the base EF, two straight lines will enclose a space: which is impossible.
Therefore the base BC will coincide with EF] and will be equal to it. [C.N. 4]
Thus the whole triangle ABC will coincide with the whole triangle DEF,
and will be equal to it.And the remaining angles will also coincide with the remaining angles and will be equal to them, the angle ABC to the angle DEF, and the angle ACB to the angle DFE.
Therefore etc.
(Being) what it was required to prove.
1-3 2. respectively. 3. the base. 6. subtend. 9. the angle BAC. 17. if the triangle be applied to..., 23. coincide. 32. [For if, when B coincides...36. coincide with EF]. 44. Therefore etc.Proposition 5.
In isosceles triangles the angles at the base are equal to one another, and, if the equal straight lines be produced further, the angles under the base will be equal to one another.
Let ABC be an isosceles triangle having the side AB
equal to the side AC; and let the straight lines BD, CE be produced further in a straight line with AB, AC. [Post. 2]
I say that the angle ABC is equal to the angle ACB, and the angle CBD to the angle BCE.
Let a point F be taken at random on BD;
from AE the greater let AG be cut off equal to AF the less; [I. 3] and let the straight lines FC, GB be joined. [Post. 1]Then, since AF is equal to AG and AB to AC,
the two sides FA, AC are equal to the two sides GA, AB, respectively;
and they contain a common angle, the angle FAG.Therefore the base FC is equal to the base GB, and the triangle AFC is equal to the triangle AGB,
and the remaining angles will be equal to the remaining angles respectively, namely those which the equal sides subtend,
that is, the angle ACF to the angle ABG,and the angle AFC to the angle AGB. [I. 4]
And, since the whole AF is equal to the whole AG,
and in these AB is equal to AC, the remainder BF is equal to the remainder CG.But FC was also proved equal to GB;
therefore the two sides BF, FC are equal to the two sides CG, GB respectively; and the angle BFC is equal to the angle CGB,
while the base BC is common to them;
therefore the triangle BFC is also equal to the triangle CGB,and the remaining angles will be equal to the remaining angles respectively, namely those which the equal sides subtend;
therefore the angle FBC is equal to the angle GCB, and the angle BCF to the angle CBG.Accordingly, since the whole angle ABG was proved equal to the angle ACF,
and in these the angle CBG is equal to the angle BCF,
the remaining angle ABC is equal to the remaining angle ACB;and they are at the base of the triangle ABC.
But the angle FBC was also proved equal to the angle GCB;
and they are under the base.Therefore etc.
Q. E. D.
2. the equal straight lines 10. Let a point F be taken at random on BD 17. the two sides FA, AC are equal to the two sides GA, AB respectively, 33. the base BC is common to them, 21Proposition 6.
If in a triangle two angles be equal to one another, the sides which subtend the equal angles will also be equal to one another.
Let ABC be a triangle having the angle ABC equal to the angle ACB;
I say that the side AB is also equal to the side AC.
For, if AB is unequal to AC, one of them is greater.
Let AB be greater; and from AB the greater let DB be cut off equal to AC the less;
let DC be joined.
[Figure]Then, since DB is equal to AC, and BC is common,
the two sides DB, BC are equal to the two sides AC, CB respectively;
and the angle DBC is equal to the angle ACB;
therefore the base DC is equal to the base AB, and the triangle DBC will be equal to the triangle ACB, the less to the greater: which is absurd. Therefore AB is not unequal to AC; it is therefore equal to it.Therefore etc.
Q. E. D.
Proposition 7.
Given two straight lines constructed on a straight line (from its extremities) and meeting in a point, there cannot be constructed on the same straight line (from its extremities), and on the same side of it, two other straight lines meeting in
another point and equal to the former two respectively, namely each to that which has the same extremity with it.
For, if possible, given two straight lines AC, CB constructed on the straight line AB and meeting at the point C, let two other straight lines
[Figure]AD, DB be constructed on the same straight line AB, on the same side of it, meeting in another point D and equal to the former two respectively, namely each to that which has the same extremity with it, so that CA is
equal to DA which has the same extremity A with it, and CB to DB which has the same extremity B with it; and let CD be joined.
Then, since AC is equal to AD,
the angle ACD is also equal to the angle ADC; [I. 5]therefore the angle ADC is greater than the angle DCB;
therefore the angle CDB is much greater than the angle DCB.Again, since CB is equal to DB,
the angle CDB is also equal to the angle DCB.But it was also proved much greater than it:
which is impossible.Therefore etc.
Q. E. D.
1-6 23 24Proposition 8.
If two triangles have the two sides equal to two sides respectively, and have also the base equal to the base, they will also have the angles equal which are contained by the equal straight lines.
Let ABC, DEF be two triangles having the two sides AB, AC equal to the two sides DE, DF respectively, namely AB to DE, and AC to DF; and let them have the base BC equal
to the base EF;
[Figure]I say that the angle BAC is also equal to the angle EDF.
For, if the triangle ABC be applied to the triangle DEF, and if the point B be placed on
the point E and the straight line BC on EF,
the point C will also coincide with F, because BC is equal to EF.Then, BC coinciding with EF,
BA, AC will also coincide with ED, DF;for, if the base BC coincides with the base EF, and the sides BA, AC do not coincide with ED, DF but fall beside them as EG, GF,
then, given two straight lines constructed on a straight line (from its extremities) and meeting in a point, there willhave been constructed on the same straight line (from its extremities), and on the same side of it, two other straight lines meeting in another point and equal to the former two respectively, namely each to that which has the same extremity with it.
But they cannot be so constructed. [I. 7]
Therefore it is not possible that, if the base BC be applied to the base EF, the sides BA, AC should not coincide with ED, DF;
they will therefore coincide,so that the angle BAC will also coincide with the angle EDF, and will be equal to it.
If therefore etc.
Q. E. D.
19. BA, AC. 26Proposition 9.
To bisect a given rectilineal angle.
Let the angle BAC be the given rectilineal angle.
Thus it is required to bisect it.
Let a point D be taken at random on AB; let AE be cut off from AC equal to AD; [I. 3] let DE be joined, and on DE let the equilateral triangle DEF be constructed; let AF be joined.
[Figure]I say that the angle BAC has been bisected by the straight line AF.
For, since AD is equal to AE, and AF is common,
the two sides DA, AF are equal to the two sides EA, AF respectively.And the base DF is equal to the base EF;
therefore the angle DAF is equal to the angle EAF. [I. 8]Therefore the given rectilineal angle BAC has been bisected by the straight line AF.
Q. E. F.
Proposition 10.
To bisect a given finite straight line.
Let AB be the given finite straight line.
Thus it is required to bisect the finite straight line AB.
Let the equilateral triangle ABC be constructed on it, [I. 1] and let the angle ACB be bisected by the straight line CD; [I. 9]
I say that the straight line AB has been bisected at the point D.
For, since AC is equal to CB, and CD is common,
[Figure]
the two sides AC, CD are equal to the two sides BC, CD respectively;
and the angle ACD is equal to the angle BCD;
therefore the base AD is equal to the base BD. [I. 4]Therefore the given finite straight line AB has been bisected at D.
Q. E. F.
Proposition 11.
To draw a straight line at right angles to a given straight line from a given point on it.
Let AB be the given straight line, and C the given point on it.
Thus it is required to draw from the point C a straight line at right angles to the straight line AB.
Let a point D be taken at random on AC;
let CE be made equal to CD; [I. 3] on DE let the equilateral triangle FDE be constructed, [I. 1] and let FC be joined;
[Figure]I say that the straight line FC has been drawn at right
angles to the given straight line AB from C the given point on it.
For, since DC is equal to CE, and CF is common,
the two sides DC, CF are equal to the two sides EC,CF respectively;
and the base DF is equal to the base FE;
therefore the angle DCF is equal to the angle ECF; [I. 8]
and they are adjacent angles.But, when a straight line set up on a straight line makes
the adjacent angles equal to one another, each of the equal angles is right; [Def. 10]
therefore each of the angles DCF, FCE is right.Therefore the straight line CF has been drawn at right angles to the given straight line AB from the given point
C on it.
Q. E. F.
10. let CE be made equal to CD.Proposition 12.
To a given infinite straight line, from a given point which is not on it, to draw a perpendicular straight line.
Let AB be the given infinite straight line, and C the given point which is not on it;
thus it is required to draw to the given infinite straight line AB, from the given point C which is not on it, a perpendicular straight line.
For let a point D be taken
at random on the other side of the straight line AB, and with centre C and distance CD let the circle EFG be described; [Post. 3]
[Figure]
let the straight line EGbe bisected at H, [I. 10] and let the straight lines CG, CH, CE be joined. [Post. 1]
I say that CH has been drawn perpendicular to the given infinite straight line AB from the given point C which is not on it.
For, since GH is equal to HE, and HC is common,
the two sides GH, HC are equal to the two sides EH, HC respectively;
and the base CG is equal to the base CE;therefore the angle CHG is equal to the angle EHC. [I. 8] And they are adjacent angles.
But, when a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is
called a perpendicular to that on which it stands. [Def. 10]
Therefore CH has been drawn perpendicular to the given infinite straight line AB from the given point C which is not on it.
Q. E. F.
2. a perpendicular straight line 10. on the other side of the straight line ABProposition 13.
If a straight line set up on a straight line make angles, it will make either two right angles or angles equal to two right angles.
For let any straight line AB set up on the straight line
CD make the angles CBA, ABD;
I say that the angles CBA, ABD are either two right angles or equal to two right angles.
[Figure]Now, if the angle CBA is equal to
the angle ABD,
they are two right angles. [Def. 10]But, if not, let BE be drawn from the point B at right angles to CD; [I. 11]
therefore the angles CBE, EBD are two right angles.Then, since the angle CBE is equal to the two angles CBA, ABE,
let the angle EBD be added to each; therefore the angles CBE, EBD are equal to the three angles CBA, ABE, EBD. [C. N. 2]Again, since the angle DBA is equal to the two angles DBE, EBA,
let the angle ABC be added to each; therefore the angles DBA. ABC are equal to the three angles DBE, EBA, ABC. [C. N. 2]But the angles CBE, EBD were also proved equal to the same three angles;
and things which are equal to the same thing are also equal to one another; [C. N. 1] therefore the angles CBE, EBD are also equal to theangles DBA, ABC.
But the angles CBE, EBD are two right angles;
therefore the angles DBA, ABC are also equal to two right angles.Therefore etc.
Q. E. D.
17. let the angle EBD be added to each,Proposition 14.
If with any straight line, and at a point on it, two straight lines not lying on the same side make the adjacent angles equal to two right angles, the two straight lines will be in a straight line with one another.
For with any straight line AB, and at the point B on it, let the two straight lines BC, BD not lying on the same side make the adjacent angles ABC, ABD equal to two right angles;
I say that BD is in a straight line with CB.
For, if BD is not in a straight line with BC, let BE be in a straight line with CB.
Then, since the straight line AB stands on the straight line CBE,
[Figure]the angles ABC, ABE are equal to two right angles. [I. 13]
But the angles ABC, ABD are also equal to two right angles;
therefore the angles CBA, ABE are equal to the angles CBA, ABD. [Post. 4 and C.N. 1]Let the angle CBA be subtracted from each;
therefore the remaining angle ABE is equal to the remaining angle ABD, [C.N. 3]
the less to the greater: which is impossible. Therefore BE is not in a straight line with CB.Similarly we can prove that neither is any other straight
line except BD. Therefore CB is in a straight line with BD.
Therefore etc.
Q. E. D.
1. If with any straight line.... 32 24. we can prove.Proposition 15.
If two straight lines cut one another, they make the vertical angles equal to one another.
For let the straight lines AB, CD cut one another at the point E;
I say that the angle AEC is equal to the angle DEB,
and the angle CEB to the angle AED.
[Figure]For, since the straight line AE stands
on the straight line CD, making the angles CEA, AED,
the angles CEA, AED are equal to two right angles [I. 13]Again, since the straight line DE stands on the straight line AB, making the angles AED, DEB,
the angles AED, DEB are equal to two right angles. [I. 13]But the angles CEA, AED were also proved equal to two right angles;
therefore the angles CEA, AED are equal to the angles AED DEB. [Post. 4 and C. N. 1] Let the angle AED be subtracted from each;therefore the remaining angle CEA is equal to the remaining angle BED. [C. N. 3]
Similarly it can be proved that the angles CEB, DEA are also equal.
Therefore etc. Q. E. D.
Porism.
[From this it is manifest that, if two straight lines cut one another, they will make the angles at the point of section equal to four right angles.
1. the vertical angles. 26. at the point of section,Proposition 16.
In any triangle, if one of the sides be produced, the exterior angle is greater than either of the interior and opposite angles.
Let ABC be a triangle, and let one side of it BC be produced to D;
I say that the exterior angle ACD is greater than either of the interior and opposite angles CBA, BAC.
Let AC be bisected at E [I. 10], and let BE be joined and produced
in a straight line to F;
[Figure]let EF be made equal to BE[I. 3], let FC be joined [Post. 1], and let AC be drawn through to G [Post. 2].
Then, since AE is equal to EC,
and BE to EF,
the two sides AE, EB are equal to the two sides CE, EF respectively; and the angle AEB is equal to the angle FEC, for they are vertical angles. [I. 15]Therefore the base AB is equal to the base FC, and the triangle ABE is equal to the triangle CFE, and the remaining angles are equal to the remaining angles respectively, namely those which the equal sides subtend; [I. 4] therefore the angle BAE is equal to the angle ECF.
But the angle ECD is greater than the angle ECF; [C. N. 5]
therefore the angle ACD is greater than the angle BAE.Similarly also, if BC be bisected, the angle BCG, that is, the angle ACD [I. 15], can be proved greater than the angle ABC as well.
Therefore etc.
Q. E. D.
1. the exterior angle, 2. the interior and opposite angles, 12. let AC be drawn through to G. 21. CFE,Proposition 17.
In any triangle two angles taken together in any manner are less than two right angles.
Let ABC be a triangle; I say that two angles of the triangle ABC taken together in any manner are less than two right angles.
For let BC be produced to D. [Post. 2]
Then, since the angle ACD is an exterior angle of the triangle ABC,
it is greater than the interior and opposite angle ABC. [I. 16]
Let the angle ACB be added to each;
therefore the angles ACD, ACB are greater than the angles ABC, BCA.
[Figure]
But the angles ACD, ACB are equal to two right angles. [I. 13]Therefore the angles ABC, BCA are less than two right angles.
Similarly we can prove that the angles BAC, ACB are also less than two right angles, and so are the angles CAB, ABC as well.
Therefore etc.
Q. E. D.
1. taken together in any manner,Proposition 18.
In any triangle the greater side subtends the greater angle.
For let ABC be a triangle having the side AC greater than AB;
I say that the angle ABC is also greater than the angle BCA.
For, since AC is greater than AB, let AD be made equal to AB [I. 3], and let BD bejoined.
Then, since the angle ADB is an exterior angle of the triangle BCD,
[Figure]it is greater than the interior and opposite angle DCB. [I. 16]
But the angle ADB is equal to the angle ABD,
since the side AB is equal to AD; therefore the angle ABD is also greater than the angle ACB; therefore the angle ABC is much greater than the angle ACB.Therefore etc.
Q. E. D.
41Proposition 19.
In any triangle the greater angle is subtended by the greater side.
Let ABC be a triangle having the angle ABC greater than the angle BCA;
I say that the side AC is also greater than the side AB.
For, if not, AC is either equal to AB or less.
Now AC is not equal to AB; for then the angle ABC would also have been equal to the angle ACB; [I. 5] but it is not;
[Figure]
therefore AC is not equal to AB.Neither is AC less than AB, for then the angle ABC would also have been less than the angle ACB; [I. 18] but it is not;
therefore AC is not less than AB.And it was proved that it is not equal either.
Therefore AC is greater than AB.Therefore etc.
Q. E. D.
Proposition 20.
In any triangle two sides taken together in any manner are greater than the remaining one.
For let ABC be a triangle; I say that in the triangle ABC two sides taken together in any manner are greater than the remaining one, namely
BA, AC greater than BC, AB, BC greater than AC, BC, CA greater than AB.For let BA be drawn through to the point D, let DA be made equal to CA, and let DC be joined.
Then, since DA is equal to AC, the angle ADC is also equal to the angle ACD; [I. 5]
[Figure]
therefore the angle BCD is greater than the angle ADC. [C.N. 5]And, since DCB is a triangle having the angle BCD greater than the angle BDC,
and the greater angle is subtended by the greater side, [I. 19] therefore DB is greater than BC.But DA is equal to AC;
therefore BA, AC are greater than BC.Similarly we can prove that AB, BC are also greater than CA, and BC, CA than AB.
Therefore etc.
Q. E. D.
42Proposition 21.
If on one of the sides of a triangle, from its extremities, there be constructed two straight lines meeting within the triangle, the straight lines so constructed will be less than the remaining two sides of the triangle, but will contain a greater
angle.
On BC, one of the sides of the triangle ABC, from its extremities B, C, let the two straight lines BD, DC be constructed meeting within the triangle;
I say that BD, DC are less than the remaining two sides
of the triangle BA, AC, but contain an angle BDC greater than the angle BAC.
[Figure]For let BD be drawn through to E.
Then, since in any triangle two sides are greater than the remaining
one, [I. 20]
therefore, in the triangle ABE, the two sides AB, AE are greater than BE.Let EC be added to each;
therefore BA, AC are greater than BE, EC.Again, since, in the triangle CED,
the two sides CE, ED are greater than CD, let DB be added to each; therefore CE, EB are greater than CD, DB.But BA, AC were proved greater than BE, EC;
therefore BA, AC are much greater than BD, DC.
Again, since in any triangle the exterior angle is greater than the interior and opposite angle, [I. 16] therefore, in the triangle CDE,
the exterior angle BDC is greater than the angle CED.For the same reason, moreover, in the triangle ABE also,
the exterior angle CEB is greater than the angle BAC.
But the angle BDC was proved greater than the angle CEB;
therefore the angle BDC is much greater than the angle BAC.Therefore etc.
Q. E. D.
2. be constructed...meeting within the triangle. 3. the straight lines so constructed.Proposition 22.
Out of three straight lines, which are equal to three given straight lines, to construct a triangle: thus it is necessary that two of the straight lines taken together in any manner should be greater than the remaining one. [I. 20]
Let the three given straight lines be A, B, C, and of these let two taken together in any manner be greater than the remaining one, namely A, B greater than C,
A, C greater than B,
and B, C greater than A; thus it is required to construct a triangle out of straight lines equal to A, B, C.
[Figure]Let there be set out a straight line DE, terminated at D but of infinite length in the direction of E, and let DF be made equal to A, FG equal to B, and GH equal to C. [I. 3]
With centre F and distance FD let the circle DKL be described; again, with centre G and distance GH let the circle KLH be described; and let KF, KG be joined;
I say that the triangle KFG has been constructed out of three straight lines equal to A, B, C.
For, since the point F is the centre of the circle DKL,
FD is equal to FK.But FD is equal to A;
therefore KF is also equal to A.Again, since the point G is the centre of the circle LKH,
GH is equal to GK.But GH is equal to C;
therefore KG is also equal to C. And FG is also equal to B;
therefore the three straight lines KF, FG, GK are equal to the three straight lines A, B, C.Therefore out of the three straight lines KF, FG, GK, which are equal to the three given straight lines A, B, C, the triangle KFG has been constructed.
Q. E. F.
2-4 2. thus it is necessary. 47Proposition 23.
On a given straight line and at a point on it to construct a rectilineal angle equal to a given rectilineal angle.
Let AB be the given straight line, A the point on it, and the angle DCE the given rectilineal angle;
thus it is required to construct on the given straight line AB, and at the point A on it, a rectilineal angle equal to the given rectilineal angle DCE.
[Figure]On the straight lines CD, CE respectively let the points D, E be taken at random; let DE be joined, and out of three straight lines which are equal to the three straight lines CD, DE, CE let the triangle AFG be constructed in such a way that CD is equal to AF, CE to AG, and further DE to FG.
Then, since the two sides DC, CE are equal to the two sides FA, AG respectively,
and the base DE is equal to the base FG, the angle DCE is equal to the angle FAG. [I. 8]Therefore on the given straight line AB, and at the point A on it, the rectilineal angle FAG has been constructed equal to the given rectilineal angle DCE.
Q. E. F.
Proposition 24.
If two triangles have the two sides equal to two sides respectively, but have the one of the angles contained by the equal straight lines greater than the other, they will also have the base greater than the base.
Let ABC, DEF be two triangles having the two sides AB, AC equal to the two sides DE, DF respectively, namely AB to DE, and AC to DF, and let the angle at A be greater than the angle at D;
I say that the base BC is also greater than the base EF.
For, since the angle BAC is greater than the angle EDF, let there be constructed, on the straight line DE, and at the point D on it, the angle EDG
equal to the angle BAC; [I. 23] let DG be made equal to either of the two straight lines AC, DF, and let EG, FG be joined.
[Figure]Then, since AB is equal to DE, and AC to DG,
the two sides BA, AC are equal to the two sides ED, DG, respectively;
and the angle BAC is equal to the angle EDG; therefore the base BC is equal to the base EG. [I. 4]Again, since DF is equal to DG,
the angle DGF is also equal to the angle DFG; [I. 5] therefore the angle DFG is greater than the angle EGF.
Therefore the angle EFG is much greater than the angle EGF.
And, since EFG is a triangle having the angle EFG
greater than the angle EGF,
and the greater angle is subtended by the greater side, [I. 19] the side EG is also greater than EF.But EG is equal to BC.
Therefore BC is also greater than EF.Therefore etc.
Q. E. D.
48
Proposition 25.If two triangles have the two sides equal to two sides respectively, but have the base greater than the base, they will also have the one of the angles contained by the equal straight lines greater than the other.
Let ABC, DEF be two triangles having the two sides AB, AC equal to the two sides DE, DF respectively, namely AB to DE, and AC to DF; and let the base BC be greater than the base EF;
I say that the angle BAC is also greater than the angle EDF.
[Figure]For, if not, it is either equal to it or less.
Now the angle BAC is not equal to the angle EDF; for then the base BC would also have been equal to the base EF, [I. 4]
but it is not; therefore the angle BAC is not equal to the angle EDF.Neither again is the angle BAC less than the angle EDF; for then the base BC would also have been less than the base EF, [I. 24]
but it is not; therefore the angle BAC is not less than the angle EDF.But it was proved that it is not equal either;
therefore the angle BAC is greater than the angle EDF.Therefore etc.
Q. E. D.
Proposition 26.
If two triangles have the two angles equal to two angles respectively, and one side equal to one side, namely, either the side adjoining the equal angles, or that subtending one of the equal angles, they will also have the remaining sides equal to
the remaining sides and the remaining angle to the remaining angle.
Let ABC, DEF be two triangles having the two angles ABC, BCA equal to the two angles DEF, EFD respectively, namely the angle ABC to the angle DEF, and the angle
BCA to the angle EFD; and let them also have one side equal to one side, first that adjoining the equal angles, namely BC to EF;
I say that they will also have the remaining sides equal to the remaining sides respectively, namely AB to DE and
AC to DF, and the remaining angle to the remaining angle, namely the angle BAC to the angle EDF.
[Figure]For, if AB is unequal to DE, one of them is greater.
Let AB be greater, and let BG be made equal to DE; and let GC be joined.
Then, since BG is equal to DE, and BC to EF, the two sides GB, BC are equal to the two sides DE, EF respectively; and the angle GBC is equal to the angle DEF;
therefore the base GC is equal to the base DF,and the triangle GBC is equal to the triangle DEF, and the remaining angles will be equal to the remaining angles, namely those which the equal sides subtend; [I. 4] therefore the angle GCB is equal to the angle DFE.
But the angle DFE is by hypothesis equal to the angle BCA;therefore the angle BCG is equal to the angle BCA, the less to the greater: which is impossible. Therefore AB is not unequal to DE, and is therefore equal to it.
But BC is also equal to EF;
therefore the two sides AB, BC are equal to the two sides DE, EF respectively, and the angle ABC is equal to the angle DEF; therefore the base AC is equal to the base DF, and the remaining angle BAC is equal to the remaining
angle EDF. [I. 4]
Again, let sides subtending equal angles be equal, as AB to DE;
I say again that the remaining sides will be equal to the remaining sides, namely AC to DF and BC to EF, and
further the remaining angle BAC is equal to the remaining angle EDF.
For, if BC is unequal to EF, one of them is greater.
Let BC be greater, if possible, and let BH be made equal to EF; let AH be joined.
Then, since BH is equal to EF, and AB to DE, the two sides AB, BH are equal to the two sides DE, EF respectively, and they contain equal angles;
therefore the base AH is equal to the base DF,
and the triangle ABH is equal to the triangle DEF,and the remaining angles will be equal to the remaining angles, namely those which the equal sides subtend; [I. 4]
therefore the angle BHA is equal to the angle EFD.But the angle EFD is equal to the angle BCA; therefore, in the triangle AHC, the exterior angle BHA is
equal to the interior and opposite angle BCA:
which is impossible. [I. 16]Therefore BC is not unequal to EF,
and is therefore equal to it.But AB is also equal to DE;
therefore the two sides AB, BC are equal to the two sides DE, EF respectively, and they contain equal angles;
therefore the base AC is equal to the base DF, the triangle ABC equal to the triangle DEF,
and the remaining angle BAC equal to the remaining angleEDF. [I. 4]
Therefore etc.
Q. E. D.
2-3. the side adjoining the equal angles, 29. is by hypothesis equal.Proposition 27.
If a straight line falling on two straight lines make the alternate angles equal to one another, the straight lines will be parallel to one another.
For let the straight line EF falling on the two straight
lines AB, CD make the alternate angles AEF, EFD equal to one another;
I say that AB is parallel to CD.
For, if not, AB, CD when produced will meet either in the direction
of B, D or towards A, C.
[Figure]Let them be produced and meet, in the direction of B, D, at G.
Then, in the triangle GEF, the exterior angle AEF is equal to the interior and opposite
angle EFG: which is impossible. [I. 16]
Therefore AB, CD when produced will not meet in the direction of B, D.
Similarly it can be proved that neither will they meet
towards A, C.
But straight lines which do not meet in either direction are parallel; [Def. 23]
therefore AB is parallel to CD.Therefore etc.
Q. E. D.
1. falling on two straight lines, 2. the alternate angles, 9. in the direction of B, D or towards A, C,Proposition 28.
If a straight line falling on two straight lines make the exterior angle equal to the interior and opposite angle on the same side, or the interior angles on the same side equal to two right angles, the straight lines will be parallel to one another.
For let the straight line EF falling on the two straight lines AB, CD make the exterior angle EGB equal to the interior and opposite angle GHD, or the interior angles on the same side, namely BGH, GHD, equal to two right angles;
I say that AB is parallel to CD.
For, since the angle EGB is equal to the angle GHD, while the angle EGB is equal to the angle AGH, [I. 15]
[Figure]
the angle AGH is also equal to the angle GHD; and they are alternate;
therefore AB is parallel to CD. [I. 27]Again, since the angles BGH, GHD are equal to two right angles, and the angles AGH, BGH are also equal to two right angles, [I. 13] the angles AGH, BGH are equal to the angles BGH, GHD.
Let the angle BGH be subtracted from each; therefore the remaining angle AGH is equal to the remaining angle GHD; and they are alternate;
therefore AB is parallel to CD. [I. 27]Therefore etc.
Q. E. D.
Proposition 29.
A straight line falling on parallel straight lines makes the alternate angles equal to one another, the exterior angle equal to the interior and opposite angle, and the interior angles on the same side equal to two right angles.
For let the straight line EF fall on the parallel straight lines AB, CD;
I say that it makes the alternate angles AGH, GHD equal, the exterior angle EGB equal to the interior and opposite angle GHD, and the interior angles on the same
side, namely BGH, GHD, equal to two right angles.
For, if the angle AGH is unequal to the angle GHD, one of them is greater.
[Figure]Let the angle AGH be greater.
Let the angle BGH be added to each; therefore the angles AGH, BGH are greater than the angles BGH, GHD.
But the angles AGH, BGH are equal to two right angles; [I. 13]
therefore the angles BGH, GHD are less than two right angles.But straight lines produced indefinitely from angles less than two right angles meet; [Post. 5]
therefore AB, CD, if produced indefinitely, will meet; but they do not meet, because they are by hypothesis parallel.
Therefore the angle AGH is not unequal to the angle GHD,
and is therefore equal to it.Again, the angle AGH is equal to the angle EGB; [I. 15]
therefore the angle EGB is also equal to the angle GHD. [C.N. 1]Let the angle BGH be added to each;
therefore the angles EGB, BGH are equal to theangles BGH, GHD. [C.N. 2]
But the angles EGB, BGH are equal to two right angles; [I. 13]
therefore the angles BGH, GHD are also equal to two right angles.Therefore etc.
Q. E. D.
23. straight lines produced indefinitely from angles less than two right angles, 26. because they are by hypothesis parallel,Proposition 30.
Straight lines parallel to the same straight line are also parallel to one another.
Let each of the straight lines AB, CD be parallel to EF; I say that AB is also parallel to CD.
For let the straight line GK fall upon them;
[Figure]Then, since the straight line GK has fallen on the parallel straight lines AB, EF,
the angle AGK is equal to the angle GHF. [I. 29]
Again, since the straight line GK has fallen on the parallel straight lines EF, CD,
the angle GHF is equal to the angle GKD. [I. 29]But the angle AGK was also proved equal to the angle GHF;
therefore the angle AGK is also equal to the angle GKD; [C.N. 1]
and they are alternate.Therefore AB is parallel to CD.
Q. E. D.
56Proposition 31.
Through a given point to draw a straight line parallel to a given straight line.
Let A be the given point, and BC the given straight line; thus it is required to draw through the point A a straight line parallel to the straight line BC.
Let a point D be taken at random on BC, and let AD be joined; on the straight line DA, and at the point A on it, let the angle DAE be constructed equal to the angle ADC [I. 23]; and let the straight line AF be produced in a straight line with EA.
[Figure]Then, since the straight line AD falling on the two straight lines BC, EF has made the alternate angles EAD, ADC equal to one another,
therefore EAF is parallel to BC. [I. 27]Therefore through the given point A the straight line EAF has been drawn parallel to the given straight line BC.
Q. E. F.
Proposition 32.
In any triangle, if one of the sides be produced, the exterior angle is equal to the two interior and opposite angles, and the three interior angles of the triangle are equal to two right angles.
Let ABC be a triangle, and let one side of it BC be produced to D;
I say that the exterior angle ACD is equal to the two interior and opposite angles CAB, ABC, and the three interior angles of the triangle ABC, BCA, CAB are equal to two right angles.
For let CE be drawn through the point C parallel to the straight line AB. [I. 31]
Then, since AB is parallel to CE,
and AC has fallen upon them, the alternate angles BAC, ACE are equal to one another. [I. 29]
[Figure]Again, since AB is parallel to CE,
and the straight line BD has fallen upon them,
the exterior angle ECD is equal to the interior and opposite angle ABC. [I. 29]But the angle ACE was also proved equal to the angle BAC;
therefore the whole angle ACD is equal to the two interior and opposite angles BAC, ABC.Let the angle ACB be added to each;
therefore the angles ACD, ACB are equal to the three angles ABC, BCA, CAB.But the angles ACD, ACB are equal to two right angles; [I. 13]
therefore the angles ABC, BCA, CAB are also equal to two right angles.Therefore etc.
Q. E. D.
Proposition 33.
The straight lines joining equal and parallel straight lines (at the extremities which are) in the same directions (respectively) are themselves also equal and parallel.
Let AB, CD be equal and parallel, and let the straight
lines AC, BD join them (at the extremities which are) in the same directions (respectively); I say that AC, BD are also equal and parallel.
Let BC be joined.
[Figure]Then, since AB is parallel to CD,
and BC has fallen upon them,
the alternate angles ABC, BCD are equal to one another. [I. 29]And, since AB is equal to CD,
and BC is common,the two sides AB, BC are equal to the two sides DC, CB; and the angle ABC is equal to the angle BCD; therefore the base AC is equal to the base BD, and the griangle ABC is equal to the triangle DCB, and the remaining angles will be equal to the remaining angles
respectively, namely those which the equal sides subtend; [I. 4] therefore the angle ACB is equal to the angle CBD.
And, since the straight line BC falling on the two straight lines AC, BD has made the alternate angles equal to one another,
AC is parallel to BD. [I. 27]
And it was also proved equal to it.
Therefore etc.
Q. E. D.
1. joining...(at the extremities which are) in the same directions (respectively). 15. DC, CBProposition 34.
In parallelogrammic areas the opposite sides and angles are equal to one another, and the diameter bisects the areas.
Let ACDB be a parallelogrammic area, and BC its diameter;
I say that the opposite sides and angles of the parallelogram ACDB are equal to one another, and the diameter BC bisects it.
[Figure]For, since AB is parallel to CD, and the straight line BC has fallen
upon them,
the alternate angles ABC, BCD are equal to one another. [I. 29]Again, since AC is parallel to BD, and BChas fallen upon them,
the alternate angles ACB, CBD are equal to one another. [I. 29]
Therefore ABC, DCB are two triangles having the two angles ABC, BCA equal to the two angles DCB, CBD respectively, and one side equal to one side, namely that
adjoining the equal angles and common to both of them, BC;
therefore they will also have the remaining sides equal to the remaining sides respectively, and the remaining angle to the remaining angle; [I. 26] therefore the side AB is equal to CD,and AC to BD,
and further the angle BAC is equal to the angle CDB.And, since the angle ABC is equal to the angle BCD,
and the angle CBD to the angle ACB, the whole angle ABD is equal to the whole angle ACD. [C.N. 2]And the angle BAC was also proved equal to the angle CDB.
Therefore in parallelogrammic areas the opposite sides and angles are equal to one another.
I say, next, that the diameter also bisects the areas.
For, since AB is equal to CD,
and BC is common, the two sides AB, BC are equal to the two sides DC, CB respectively;
and the angle ABC is equal to the angle BCD; therefore the base AC is also equal to DB,and the triangle ABC is equal to the triangle DCB. [I. 4]
Therefore the diameter BC bisects the parallelogram ACDB.
Q. E. D.
59 17, 18, 40. DCBProposition 35.
Parallelograms which are on the same base and in the same parallels are equal to one another.
Let ABCD, EBCF be parallelograms on the same base BC and in the same parallels AF, BC;
I say that ABCD is equal to the parallelogram EBCF.
For, since ABCD is a parallelogram,
AD is equal to BC. [I. 34]For the same reason also
EF is equal to BC,so that AD is also equal to EF; [C.N. 1]
and DE is common;
therefore the whole AE is equal to the whole DF. [C.N. 2]But AB is also equal to DC; [I. 34] therefore the two sides EA, AB are equal to the two sides
FD, DC respectively,
[Figure]
and the angle FDC is equal to the angle EAB, the exterior to the interior; [I. 29] therefore the base EB is equalto the base FC, and the triangle EAB will be equal to the triangle FDC. [I. 4]
Let DGE be subtracted from each; therefore the trapezium ABGD which remains is equal to the trapezium EGCF which remains. [C.N. 3]
Let the triangle GBC be added to each; therefore the whole parallelogram ABCD is equal to the whole parallelogram EBCF. [C.N. 2]
Therefore etc.
Q. E. D.
21. FDC. 22. Let DGE be subtracted.Proposition 36.
Parallelograms which are on equal bases and in the same parallels are equal to one another.
Let ABCD, EFGH be parallelograms which are on equal bases BC, FG and in the same parallels AH, BG;
[Figure]
I say that the parallelogram ABCD is equal to EFGH.For let BE, CH be joined.
Then, since BC is equal to FG while FG is equal to EH,
BC is also equal to EH. [C.N. 1]But they are also parallel.
And EB, HC join them; but straight lines joining equal and parallel straight lines (at the extremities which are) in the same directions (respectively) are equal and parallel. [I. 33]
Therefore EBCH is a parallelogram. [I. 34]
And it is equal to ABCD; for it has the same base BC with it, and is in the same parallels BC, AH with it. [I. 35]
For the same reason also EFGH is equal to the same EBCH; [I. 35] so that the parallelogram ABCD is also equal to EFGH. [C.N. 1]
Therefore etc. Q. E. D.
Proposition 37.
Triangles which are on the same base and in the same parallels are equal to one another.
Let ABC, DBC be triangles on the same base BC and in the same parallels AD, BC;
I say that the triangle ABC is equal to the triangle DBC.
Let AD be produced in both directions to E, F; through B let BE be drawn parallel to CA, [I. 31]
and through C let CF be drawn parallel to BD. [I. 31]
[Figure]Then each of the figures EBCA, DBCF is a parallelogram; and they are equal,
for they are on the same base BC and in the same parallels BC, EF. [I. 35]
Moreover the triangle ABC is half of the parallelogram EBCA; for the diameter AB bisects it. [I. 34]
And the triangle DBC is half of the parallelogram DBCF;
for the diameter DC bisects it. [I. 34]
[But the halves of equal things are equal to one another.]
Therefore the triangle ABC is equal to the triangle DBC.
Therefore etc.
Q. E. D.
63Proposition 38.
Triangles which are on equal bases and in the same parallels are equal to one another.
Let ABC, DEF be triangles on equal bases BC, EF and in the same parallels BF, AD; I say that the triangle ABC is equal to the triangle DEF.
[Figure]For let AD be produced in both directions to G, H; through B let BG be drawn parallel to CA, [I. 31] and through F let FH be drawn parallel to DE.
Then each of the figures GBCA, DEFH is a parallelogram; and GBCA is equal to DEFH; for they are on equal bases BC, EF and in the same parallels BF, GH. [I. 36]
Moreover the triangle ABC is half of the parallelogram GBCA; for the diameter AB bisects it. [I. 34]
And the triangle FED is half of the parallelogram DEFH; for the diameter DF bisects it. [I. 34]
[But the halves of equal things are equal to one another.]
Therefore the triangle ABC is equal to the triangle DEF.
Therefore etc.
Q. E. D.
Proposition 39.
Equal triangles which are on the same base and on the same side are also in the same parallels.
Let ABC, DBC be equal triangles which are on the same base BC and on the same side of it;
[I say that they are also in the same parallels.]
And [For] let AD be joined; I say that AD is parallel to BC.
For, if not, let AE be drawn through the point A parallel to the straight line
BC, [I. 31] and let EC be joined.
[Figure]Therefore the triangle ABC is equal to the triangle EBC; for it is on the same base BC with it and in the same
parallels. [I. 37]
But ABC is equal to DBC;
therefore DBC is also equal to EBC, [C.N. 1] the greater to the less: which is impossible.Therefore AE is not parallel to BC.
Similarly we can prove that neither is any other straight line except AD;
therefore AD is parallel to BC.Therefore etc.
Q. E. D.
64
[Proposition 40.Equal triangles which are on equal bases and on the same side are also in the same parallels.
Let ABC, CDE be equal triangles on equal bases BC, CE and on the same side.
I say that they are also in the same parallels.
For let AD be joined; I say that AD is parallel to BE.
For, if not, let AF be drawn through A parallel to BE [I. 31], and let FE be joined.
[Figure]Therefore the triangle ABC is equal to the triangle FCE; for they are on equal bases BC, CE and in the same parallels BE, AF. [I. 38]
But the triangle ABC is equal to the triangle DCE;
therefore the triangle DCE is also equal to the triangle FCE, [C.N. 1] the greater to the less: which is impossible. Therefore AF is not parallel to BE.Similarly we can prove that neither is any other straight line except AD;
therefore AD is parallel to BE.Therefore etc. Q. E. D.]
Proposition 41.
If a parallelogram have the same base with a triangle and be in the same parallels, the parallelogram is double of the triangle.
For let the parallelogram ABCD have the same base BC with the triangle EBC, and let it be in the same parallels BC, AE;
I say that the parallelogram ABCD is double of the triangle BEC.
For let AC be joined.
Then the triangle ABC is equal to the triangle EBC; for it is on the same base BC with it and in the same parallels BC, AE. [I. 37]
[Figure]But the parallelogram ABCD is double of the triangle ABC;
for the diameter AC bisects it; [I. 34]
so that the parallelogram ABCD is also double of the triangle EBC.Therefore etc.
Q. E. D.
Proposition 42.
To construct, in a given rectilineal angle, a parallelogram equal to a given triangle.
Let ABC be the given triangle, and D the given rectilineal angle; thus it is required to construct in the rectilineal angle D a parallelogram equal to the triangle ABC.
[Figure]Let BC be bisected at E, and let AE be joined; on the straight line EC, and at the point E on it, let the angle CEF be constructed equal to the angle D; [I. 23] through A let AG be drawn parallel to EC, and [I. 31] through C let CG be drawn parallel to EF.
Then FECG is a parallelogram.
And, since BE is equal to EC,
the triangle ABE is also equal to the triangle AEC, for they are on equal bases BE, EC and in the same parallels BC, AG; [I. 38] therefore the triangle ABC is double of the triangle AEC.But the parallelogram FECG is also double of the triangle AEC, for it has the same base with it and is in the same parallels with it; [I. 41]
therefore the parallelogram FECG is equal to the triangle ABC.And it has the angle CEF equal to the given angle D.
Therefore the parallelogram FECG has been constructed equal to the given triangle ABC, in the angle CEF which is equal to D. Q. E. F.
Proposition 43.
In any parallelogram the complements of the parallelograms about the diameter are equal to one another.
Let ABCD be a parallelogram, and AC its diameter; and about AC let EH, FG be parallelograms, and BK, KD
the so-called complements;
I say that the complement BK is equal to the complement KD.
For, since ABCD is a parallelogram, and AC its diameter,
the triangle ABC is equal tothe triangle ACD. [I. 34]
Again, since EH is a parallelogram, and AK is its diameter,
the triangle AEK is equal to the triangle AHK.
[Figure]For the same reason
the triangle KFC is also equal to KGC.Now, since the triangle AEK is equal to the triangle AHK,
and KFC to KGC,the triangle AEK together with KGC is equal to the triangle AHK together with KFC. [C.N. 2]
And the whole triangle ABC is also equal to the whole ADC; therefore the complement BK which remains is equal to the
complement KD which remains. [C.N. 3]
Therefore etc.
Q. E. D.
65 4. and about AC....Proposition 44.
To a given straight line to apply, in a given rectilineal angle, a parallelogram equal to a given triangle.
Let AB be the given straight line, C the given triangle and D the given rectilineal angle;
thus it is required to apply to the given straight line AB, in an angle equal to the angle D, a parallelogram equal to the given triangle C.
Let the parallelogram BEFG be constructed equal to the triangle C, in the angle EBG which is equal to D [I. 42];
let it be placed so that BE is in a straight line with AB; let FG be drawn through to H, and let AH be drawn through A parallel to either BG or EF. [I. 31]
Let HB be joined.
[Figure]Then, since the straight line HF falls upon the parallels
AH, EF,
the angles AHF, HFE are equal to two right angles. [I. 29]
Therefore the angles BHG, GFE are less than two right angles; and straight lines produced indefinitely from angles less thantwo right angles meet; [Post. 5]
therefore HB, FE, when produced, will meet.Let them be produced and meet at K; through the point K let KL be drawn parallel to either EA or FH, [I. 31] and let HA, GB be produced to the points L, M.
Then HLKF is a parallelogram, HK is its diameter, and AG, ME are parallelograms. and LB, BF the so-called complements, about HK;
therefore LB is equal to BF. [I. 43]But BF is equal to the triangle C;
therefore LB is also equal to C. [C.N. 1]
And, since the angle GBE is equal to the angle ABM, [I. 15]
while the angle GBE is equal to D, the angle ABM is also equal to the angle D.Therefore the parallelogram LB equal to the given triangle
C has been applied to the given straight line AB, in the angle ABM which is equal to D.
Q. E. F.
14. since the straight line HF falls....Proposition 45.
To construct, in a given rectilineal angle, a parallelogram equal to a given rectilineal figure.
Let ABCD be the given rectilineal figure and E the given rectilineal angle;
thus it is required to construct, in the given angle E, a parallelogram equal to the rectilineal figure ABCD.
[Figure]Let DB be joined, and let the parallelogram FH be constructed equal to the triangle ABD, in the angle HKF which is equal to E; [I. 42]
let the parallelogram GM equal to the triangle DBC be applied to the straight line GH, in the angle GHM which is equal to E. [I. 44]
Then, since the angle E is equal to each of the angles HKF, GHM,
the angle HKF is also equal to the angle GHM. [C.N. 1]
Let the angle KHG be added to each; therefore the angles FKH, KHG are equal to the angles KHG, GHM.
But the angles FKH, KHG are equal to two right angles; [I. 29]
therefore the angles KHG, GHM are also equal to two right angles.
Thus, with a straight line GH, and at the point H on it, two straight lines KH, HM not lying on the same side make the adjacent angles equal to two right angles;
therefore KH is in a straight line with HM. [I. 14]
And, since the straight line HG falls upon the parallels KM, FG, the alternate angles MHG, HGF are equal to one another. [I. 29]
Let the angle HGL be added to each;
therefore the angles MHG, HGL are equal to the angles HGF, HGL. [C.N. 2]
But the angles MHG, HGL are equal to two right angles; [I. 29] therefore the angles HGF, HGL are also equal to two right angles. [C.N. 1]
Therefore FG is in a straight line with GL. [I. 14]
And, since FK is equal and parallel to HG, [I. 34]
and HG to ML also,
KF is also equal and parallel to ML; [C.N. 1; I. 30] and the straight lines KM, FL join them (at their extremities);therefore KM, FL are also equal and parallel. [I. 33]
Therefore KFLM is a parallelogram.And, since the triangle ABD is equal to the parallelogram FH,
and DBC to GM,the whole rectilineal figure ABCD is equal to the whole parallelogram KFLM.
Therefore the parallelogram KFLM has been constructed equal to the given rectilineal figure ABCD, in the angle FKM which is equal to the given angle E.
Q. E. F.
2, 3, 6, 45, 48. rectilineal figure, in the GreekProposition 46.
On a given straight line to describe a square.
Let AB be the given straight line; thus it is required to describe a square on the straight line AB.
[Figure]Let AC be drawn at right angles to the straight line AB from the point A on it [I. 11], and let AD be made equal to AB; through the point D let DE be drawn
parallel to AB, and through the point B let BE be drawn parallel to AD. [I. 31]
Therefore ADEB is a parallelogram;
therefore AB is equal to DE, and AD to BE. [I. 34]But AB is equal to AD;
therefore the four straight lines BA, AD, DE, EB are equal to one another;
therefore the parallelogram ADEB is equilateral.I say next that it is also right-angled.
For, since the straight line AD falls upon the parallels
AB, DE,
the angles BAD, ADE are equal to two right angles. [I. 29]But the angle BAD is right;
therefore the angle ADE is also right.And in parallelogrammic areas the opposite sides and
angles are equal to one another; [I. 34]
therefore each of the opposite angles ABE, BED is also right. Therefore ADEB is right-angled.And it was also proved equilateral.
Therefore it is a square; and it is described on the straight line AB.
Q. E. F.
1, 3, 30Proposition 47.
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
Let ABC be a right-angled triangle having the angle
BAC right;
I say that the square on BC is equal to the squares on BA, AC.
For let there be described on BC the square BDEC,
and on BA, AC the squares GB, HC; [I. 46] through A let AL be drawn parallel to either BD or CE, and let AD, FC be joined.
[Figure]Then, since each of the angles BAC, BAG is right, it follows that with a straight line BA, and at the point A on it, the two straight lines
AC, AG not lying on the same side make the adjacent angles equal to two right angles;
therefore CA is in a straight line with AG. [I. 14]For the same reason
BA is also in a straight line with AH.And, since the angle DBC is equal to the angle FBA: for each is right: let the angle ABC be added to each;
therefore the whole angle DBA is equal to the whole angle FBC. [C.N. 2]
And, since DB is equal to BC, and FB to BA, the two sides AB, BD are equal to the two sides FB, BC respectively,
and the angle ABD is equal to the angle FBC; therefore the base AD is equal to the base FC, and the triangle ABD is equal to the triangle FBC. [I. 4]
Now the parallelogram BL is double of the triangle ABD, for they have the same base BD and are in the same parallels
BD, AL. [I. 41]
And the square GB is double of the triangle FBC, for they again have the same base FB and are in the same parallels FB, GC. [I. 41]
[But the doubles of equals are equal to one another.]
Therefore the parallelogram BL is also equal to the square GB.
Similarly, if AE, BK be joined, the parallelogram CL can also be proved equal to the square HC;
therefore the whole square BDEC is equal to the two squares GB, HC. [C.N. 2]
And the square BDEC is described on BC,
and the squares GB, HC on BA, AC.Therefore the square on the side BC is equal to the
squares on the sides BA, AC.
Therefore etc.
Q. E. D.
1. the square on 71 33. the two sides AB, BD.... 73Proposition 48.
If in a triangle the square on one of the sides be equal to the squares on the remaining two sides of the triangle, the angle contained by the remaining two sides of the triangle is right.
For in the triangle ABC let the square on one side BC be equal to the squares on the sides BA, AC;
I say that the angle BAC is right.
For let AD be drawn from the point A at right angles to the straight line AC, let AD be made equal to BA, and let DC be joined.
Since DA is equal to AB, the square on DA is also equal to the square on AB.
[Figure]Let the square on AC be added to each; therefore the squares on DA, AC are equal to the squares on BA, AC.
But the square on DC is equal to the squares on DA, AC, for the angle DAC is right; [I. 47] and the square on BC is equal to the squares on BA, AC, for this is the hypothesis;
therefore the square on DC is equal to the square on BC, so that the side DC is also equal to BC.And, since DA is equal to AB, and AC is common,
the two sides DA, AC are equal to the two sides BA, AC;
and the base DC is equal to the base BC;
therefore the angle DAC is equal to the angle BAC. [I. 8]
But the angle DAC is right;
therefore the angle BAC is also right.Therefore etc.
Q. E. D.
NOTES
1. On a given finite straight line. The Greek usage differs from ours in that the definite article is employed in such a phrase as this where we have the indefinite. epi tês dotheisês eutheias peperasmenês, “on the given finite straight line,” i.e. the finite straight line which we choose to take.
3. Let AB be the given finite straight line. To be strictly literal we should have to translate in the reverse order “let the given finite straight line be the (straight line) AB”; but this order is inconvenient in other cases where there is more than one datum, e.g. in the setting-out of I. 2, “let the given point be A, and the given straight line BC,” the awkwardness arising from the omission of the verb in the second clause. Hence I have, for clearness' sake, adopted the other order throughout the book.
8. let the circle BCD be described. Two things are here to be noted, (1) the elegant and practically universal use of the perfect passive imperative in constructions, gegraphthô meaning of course “let it have been described” or “suppose it described,” (2) the impossibility of expressing shortly in a translation the force of the words in their original order. kuklos gegraphthô o BGD means literally “let a circle have been described, the (circle, namely, which I denote by) BCD.” Similarly we have lower down “let straight lines, (namely) the (straight lines) CA, CB, be joined,” epezeuchthôsan eutheiai ai GA, GB. There seems to be no practicable alternative, in English, but to translate as I have done in the text.
13. from the point C.... Euclid is careful to adhere to the phraseology of Postulate 1 except that he speaks of “joining” (epezeuchthôsan) instead of “drawing” (graphein). He does not allow himself to use the shortened expression “let the straight line FC be joined” (without mention of the points F, C) until I. 5.
20. each of the straight lines CA, CB , hekatera tôn GA, GB and 24. the three straight lines CA, AB, BC, hai treis hai GA, AB, BG. I have, here and in all similar expressions, inserted the words “straight lines” which are not in the Greek. The possession of the inflected definite article enables the Greek to omit the words, but this is not possible in English, and it would scarcely be English to write “each of CA, CB” or “the three CA, AB, BC.”
1. (as an extremity). I have inserted these words because “to place a straight line at a given point” (pros tôi dothenti sêmeiôi) is not quite clear enough, at least in English.
11. Let the straight lines AE, BF be produced.... It will be observed that in this first application of Postulate 2, and again in I. 5, Euclid speaks of the continuation of the straight line as that which is produced in such cases, ekbeblêsthôsan and prosekbeblêsthôsan meaning little more than drawing straight lines “in a straight line with” the given straight lines. The first place in which Euclid uses phraseology exactly corresponding to ours when speaking of a straight line being produced is in I. 16: “let one side of it, BC, be produced to D” (prosekbeblêsthô autou mia pleura hê BG epi to D).
23. the remainder AL...the remainder BG. The Greek expressions are loipê hê AL and loipêi têi BH, and the literal translation would be “AL (or BG) remaining,” but the shade of meaning conveyed by the position of the definite article can hardly be expressed in English.
1-3 It is a fact that Euclid's enunciations not infrequently leave something to be desired in point of clearness and precision. Here he speaks of the triangles having “the angle equal to the angle, namely the angle contained by the equal straight lines” (tên gônian têi gôniai isên echêi tên hupo tôn isôn eutheiôn periechomenên), only one of the two angles being described in the latter expression (in the accusative), and a similar expression in the dative being left to be understood of the other angle. It is curious too that, after mentioning two “sides,” he speaks of the angles contained by the equal “straight lines,” not “sides.” It may be that he wished to adhere scrupulously, at the outset, to the phraseology of the definitions, where the angle is the inclination to one another of two lines or straight lines. Similarly in the enunciation of I. 5 he speaks of producing the equal “straight lines” as if to keep strictly to the wording of Postulate 2.
2. respectively. I agree with Mr H. M. Taylor (Euclid, p. ix) that it is best to abandon the traditional translation of “each to each,” which would naturally seem to imply that all the four magnitudes are equal rather than (as the Greek ekatera ekaterai does) that one is equal to one and the other to the other.
3. the base. Here we have the word base used for the first time in the Elements. Proclus explains it (p. 236, 12-15) as meaning (1), when no side of a triangle has been mentioned before, the side “which is on a level with the sight” (tên pros têi opsei keimenên), and (2), when two sides have already been mentioned, the third side. Proclus thus avoids the mistake made by some modern editors who explain the term exclusively with reference to the case where two sides have been mentioned before. That this is an error is proved (1) by the occurrence of the term in the enunciations of I. 37 etc. about triangles on the same base and equal bases, (2) by the application of the same term to the bases of parallelograms in I. 35 etc. The truth is that the use of the term must have been suggested by the practice of drawing the particular side horizontally, as it were, and the rest of the figure above it. The base of a figure was therefore spoken of, primarily, in the same sense as the base of anything else, e.g. of a pedestal or column; but when, as in I. 5, two triangles were compared occupying other than the normal positions which gave rise to the name, and when two sides had been previously mentioned, the base was, as Proclus says, necessarily the third side.
6. subtend. hupoteinein hupo, “to stretch under,” with accusative.
9. the angle BAC. The full Greek expression would be hê hupo tôn BA, AG periechomenê gônia, “the angle contained by the (straight lines) BA, AC.” But it was a common practice of Greek geometers, e.g. of Archimedes and Apollonius (and Euclid too in Books X.--XIII.), to use the abbreviation hai BAG for hai BA, AG, “the (straight lines) BA, AC.” Thus, on periechomenê being dropped, the expression would become first hê hupo tôn BAG gônia, then hê hupo BAG gônia, and finally hê hupo BAG, without gônia, as we regularly find it in Euclid.
17. if the triangle be applied to..., 23. coincide. The difference between the technical use of the passive epharmozesthai “to be applied (to),” and of the active epharmozein “to coincide (with)” has been noticed above (note on Common Notion 4, pp. 224-5).
32. [For if, when B coincides...36. coincide with EF]. Heiberg (Paralipomena su Euklid in Hermes, XXXVIII., 1903, p. 56) has pointed out, as a conclusive reason for regarding these words as an early interpolation, that the text of an-Nair?z? (Codex Leidensis 399, 1, ed. Besthorn-Heiberg, p. 55) does not give the words in this place but after the conclusion Q.E.D., which shows that they constitute a scholium only. They were doubtless added by some commentator who thought it necessary to explain the immediate inference that, since B coincides with E and C with F, the straight line BC coincides with the straight line EF, an inference which really follows from the definition of a straight line and Post. 1; and no doubt the Postulate that “Two straight lines cannot enclose a space” (afterwards placed among the Common Notions) was interpolated at the same time.
44. Therefore etc. Where (as here) Euclid's conclusion merely repeats the enunciation word for word, I shall avoid the repetition and write “Therefore etc.” simply.
2. the equal straight lines (meaning the equal sides). Cf. note on the similar expression in Prop. 4, lines 2, 3.
10. Let a point F be taken at random on BD , eilêphthô epi tês BD tuchon sêmeion to Z, where tuchon sêmeionmeans “a chance point.”
17. the two sides FA, AC are equal to the two sides GA, AB respectively, duo hai ZA, AG dusi tais ÊA, AB isai eisin hekatera hekaterai. Here, and in numberless later passages, I have inserted the word “sides” for the reason given in the note on I. 1, line 20. It would have been permissible to supply either “straight lines” or “sides”; but on the whole “sides” seems to be more in accordance with the phraseology of I. 4.
33. the base BC is common to them, i.e., apparently, common to the angles, as the autôn in basis autôn koinê can only refer to gônia and gôniai preceding. Simson wrote “and the base BC is common to the two triangles BFC, CGB”; Todhunter left out these words as being of no use and tending to perplex a beginner. But Euclid evidently chose to quote the conclusion of I. 4 exactly; the first phrase of that conclusion is that the bases (of the two triangles) are equal, and, as the equal bases are here the same base, Euclid naturally substitutes the word “common” for “equal.”
21 As “(Being) what it was required to prove” (or “do”) is somewhat long, I shall henceforth write the time-honoured “Q. E. D.” and “Q. E. F.” for hoper edei deixai and hoper edei poiêsai.
1-6 In an English translation of the enunciation of this proposition it is absolutely necessary, in order to make it intelligible, to insert some words which are not in the Greek. The reason is partly that the Greek enunciation is itself very elliptical, and partly that some words used in it conveyed more meaning than the corresponding words in English do. Particularly is this the case with ou sustathêsontai epi “there shall not be constructed upon,” since sunistasthai is the regular word for constructing a triangle in particular. Thus a Greek would easily understahd sustathêsontai epi as meaning the construction of two lines forming a triangle on a given straight line as base; whereas to “construct two straight lines on a straight line” is not in English sufficiently definite unless we explain that they are drawn from the ends of the straight line to meet at a point. I have had the less hesitation in putting in the words “from its extremities” because they are actually used by Euclid in the somewhat similar enunciation of I. 21.
How impossible a literal translation into English is, if it is to convey the meaning of the enunciation intelligibly, will be clear from the following attempt to render literally: “On the same straight line there shall not be constructed two other straight lines equal, each to each, to the same two straight lines, (terminating) at different points on the same side, having the same extremities as the original straight lines” (epi tês autês eutheias duo tais autais eutheiais allai duo eutheiai isai hekatera hekatera ou sustathêsontai pros allôi kai allôi sêmeiôi epi ta auta merê ta auta perata echousai tais ex archês eutheiais).
The reason why Euclid allowed himself to use, in this enunciation, language apparently so obscure is no doubt that the phraseology was traditional and therefore, vague as it was, had a conventional meaning which the contemporary geometer well understood. This is proved, I think, by the occurrence in Aristotle (Meteorologica III. 5, 376 a 2 sqq.) of the very same, evidently technical, expressions. Aristotle is there alluding to the theorem given by Eutocius from Apollonius' Plane Loci to the effect that, if H, K be two fixed points and M such a variable point that the ratio of MH to MK is a given ratio (not one of equality), the locus of M is a circle. (For an account of this theorem see note on VI. 3 below.) Now Aristotle says “The lines drawn up from H, K in this ratio cannot be constructed to two different points of the semicircle A” (ai oun apo tôn ÊK anagomenai grammai en toutôi tôi logôi ou sustathêsoutai tou eph ôi A hêmikukliou pros allo kai allo sêmeion).
If a paraphrase is allowed instead of a translation adhering as closely as possible to the original, Simson's is the best that could be found, since the fact that the straight lines form triangles on the same base is really conveyed in the Greek. Simson's enunciation is, Upon the same base, and on the same side of it, there cannot be two triangles that have their sides which are terminated in one extremity of the base equal to one another, and likewise those which are terminated at the other extremity. Th. Taylor (the translator of Proclus) attacks Simson's alteration as “indiscreet” and as detracting from the beauty and accuracy of Euclid's enunciation which are enlarged upon by Proclus in his commentary. Yet, when Taylor says “Whatever difficulty learners may find in conceiving this proposition abstractedly is easily removed by its exposition in the figure,” he really gives his case away. The fact is that Taylor, always enthusiastic over his author, was nettled by Simson's slighting remarks on Proclus' comments on the proposition. Simson had said, with reference to Proclus' explanation of the bearing of the second part of I. 5 on I. 7, that it was not “worth while to relate his trifles at full length,” to which Taylor retorts “But Mr Simson was no philosopher; and therefore the greatest part of these Commentaries must be considered by him as trifles, from the want of a philosophic genius to comprehend their meaning, and a taste superior to that of a mere mathematician, to discover their beauty and elegance.”
23 It would be natural to insert here the step “but the angle ACD is greater than the angle BCD. [C.N. 5].”
24 much greater, literally “greater by much” (pollôi meizôn). Simson and those who follow him translate: “much more then is the angle BDC greater than the angle BCD,” but the Greek for this would have to be pollôi (or polu ) mallon esti...meizôn. pollôi mallon, however, though used by Apollonius, is not, apparently, found in Euclid or Archimedes.
19. BA, AC. The text has here “BA, CA.”
26 fall beside them. The Greek has the future, parallaxousi. parallattô means “to pass by without touching,” “to miss” or “to deviate.”
10. let CE be made equal to CD. The verb is keisthô which, as well as the other parts of keimai, is constantly used for the passive of tithêmi “to place”; and the latter word is constantly used in the sense of making, e.g., one straight line equal to another straight line.
2. a perpendicular straight line , katheton eutheian grammhên. This is the full expression for a perpendicular, kathetos meaning let fall or let down, so that the expression corresponds to our plumb-line. hê kathetos is however constantly used alone for a perpendicular, grammhê being understood.
10. on the other side of the straight line AB , literally “towards the other parts of the straight line AB,” epi ta hetera merê tês AB. Cf. “on the same side” (epi ta auta merê) in Post. 5 and “in both directions” (eph hekatera ta mherê) in Def. 23.
17. let the angle EBD be added to each, literally “let the angle EBD be added (so as to be) common,” koinê proskeisthô hê hupo EBD. Similarly koinê aphêrêsthô is used of subtracting a straight line or angle from each of two others. “Let the common angle EBD be added” is clearly an inaccurate translation, for the angle is not common before it is added, i.e. the koinê is proleptic. “Let the common angle be subtracted” as a translation of koinê aphêrêsthô would be less unsatisfactory, it is true, but, as it is desirable to use corresponding words when translating the two expressions, it seems hopeless to attempt to keep the word “common,” and I have therefore said “to each” and “from each” simply.
1. If with any straight line.... There is no greater difficulty in translating the works of the Greek geometers than that of accurately giving the force of prepositions. pros, for instance, is used in all sorts of expressions with various shades of meaning. The present enunciation begins ean pros tini eutheiai kai tôi pros autê sêmeiôi, and it is really necessary in this one sentence to translate pros by three different words, with, at, and on. The first pros must be translated by with because two straight lines “make” an angle with one another. On the other hand, where the similar expression pros têi dotheisê eutheiai occurs in I. 23, but it is a question of “constructing” an angle (susthêsasthai), we have to say “to construct on a given straight line.” Against would perhaps be the English word coming nearest to expressing all these meanings of pros, but it would be intolerable as a translation.
32 Todhunter points out that for the inference in this line Post. 4, that all right angles are equal, is necessary as well as the Common Notion that things which are equal to the same thing (or rather, here, to equal things) are equal. A similar remark applies to steps in the proofs of I. 15 and I. 28.
24. we can prove. The Greek expresses this by the future of the verb, deixomen, “we shall prove,” which however would perhaps be misleading in English.
1. the vertical angles. The difference between adjacent angles (hai ephexês gôniai) and vertical angles (hai kata koruphên gôniai) is thus explained by Proclus (p. 298, 14-24). The first term describes the angles made by two straight lines when one only is divided by the other, i.e. when one straight line meets another at a point which is not either of its extremities, but is not itself produced beyond the point of meeting. When the first straight line is produced, so that the lines cross at the point, they make two pairs of vertical angles (which are more clearly described as vertically opposite angles), and which are so called because their convergence is from opposite directions to one point (the intersection of the lines) as vertex (koruphê).
26. at the point of section, literally “at the section,” pros têi tomê.
1. the exterior angle, literally “the outside angle,”'w ektos gwnia.
2. the interior and opposite angles, tôn entos kai apenantion gôniôn.
12. let AC be drawn through to G. The word is diwchthw, a variation on the more usual ekbeblw sthw, “let it be produced.”
21. CFE, in the text “FEC.”
1. taken together in any manner, pantê metalambanomenai, i.e. any pair added together.
41 In the enunciation of this proposition we have hupoteinein (“subtend”) used with the simple accusative instead of the more usual hupo with accusative. The latter construction is used in the enunciation of I. 19, which otherwise only differs from that of I. 18 in the order of the words. The point to remember in order to distinguish the two is that the datum comes first and the quaesitum second, the datum being in this proposition the greater side and in the next the greater angle. Thus the enunciations are (I. 18) pantos trigwnou 'w meizwn pleura twn meizona gwnian hupoteinei and (I. 19) pantos trigônou hupo tên meizona gônian hê meizôn pleura hupoteinei. In order to keep the proper order in English we must use the passive of the verb in I. 19. Aristotle quotes the result of I. 19, using the exact wording, 'upo gar twn meizw gwnian 'upoteinei (Meteorologica III. 5, 376 a 12).
42 It was the habit of the Epicureans, says Proclus (p. 322), to ridicule this theorem as being evident even to an ass and requiring no proof, and their allegation that the theorem was “known” (gnôrimon) even to an ass was based on the fact that, if fodder is placed at one angular point and the ass at another, he does not, in order to get to his food, traverse the two sides of the triangle but only the one side separating them (an argument which makes Savile exclaim that its authors were “digni ipsi, qui cum Asino foenum essent,” p. 78). Proclus replies truly that a mere perception of the truth of the theorem is a different thing from a scientific proof of it and a knowledge of the reason why it is true. Moreover, as Simson says, the number of axioms should not be increased without necessity.
2. be constructed...meeting within the triangle. The word “meeting” is not in the Greek, where the words are entos sustathwsin. sunistasthai is the word used of constructing two straight lines to a point (cf. I. 7) or so as to form a triangle; but it is necessary in English to indicate that they meet.
3. the straight lines so constructed. Observe the elegant brevity of the Greek hai sustatheisai.
2-4 This is the first case in the Elements of a diorismos to a problem in the sense of a statement of the conditions or limits of the possibility of a solution. The criterion is of course supplied by the preceding proposition.
2. thus it is necessary. This is usually translated (e.g. by Williamson and Simson) “But it is necessary,” which is however inaccurate, since the Greek is not dei de but dei dê. The words are the same as those used to introduce the diorismos in the other sense of the “definition” or “particular statement” of a construction to be effected. Hence, as in the latter case we say “thus it is required” (e.g. to bisect the finite straight line AB, I. 10), we should here translate “thus it is necessary.”
47 To this enunciation all the MSS. and Boethius add, after the diorismos, the words “because in any triangle two sides taken together in any manner are greater than the remaining one.” But this explanation has the appearance of a gloss, and it is omitted by Proclus and Campanus. Moreover there is no corresponding addition to the diorismos of VI. 28.
48 I have naturally left out the well-known words added by Simson in order to avoid the necessity of considering three cases: “Of the two sides DE, DF let DE be the side which is not greater than the other.” I doubt whether Euclid could have been induced to insert the words himself, even if it had been represented to him that their omission meant leaving two possible cases out of consideration. His habit and that of the great Greek geometers was, not to set out all possible cases, but to give as a rule one case, generally the most difficult, as here, and to leave the others to the reader to work out for himself. We have already seen one instance in I. 7.
2-3. the side adjoining the equal angles, pleuran tên pros tais isais gôniais.
29. is by hypothesis equal. 'upokeitai isê, according to the elegant Greek idiom. hupokeimai is used for the passive of 'upotithêmi, as keimai is used for the passive of tiqwmi, and so with the other compounds. Cf. proskeisqai, “to be added.”
1. falling on two straight lines, eis duo eutheias empiptousa, the phrase being the same as that used in Post. 5, meaning a transversal.
2. the alternate angles, hai enallax gôniai. Proclus (p. 357, 9) explains that Euclid uses the word alternate (or, more exactly, alternately, enallax) in two connexions, (1) of a certain transformation of a proportion, as in Book V. and the arithmetical Books, (2) as here, of certain of the angles formed by parallels with a straight line crossing them. Alternate angles are, according to Euclid as interpreted by Proclus, those which are not on the same side of the transversal, and are not adjacent, but are separated by the transversal, both being within the parallels but one “above” and the other “below.” The meaning is natural enough if we imagine the four internal angles to be taken in cyclic order and alternate angles to be any two of them not successive but separated by one angle of the four.
9. in the direction of B, D or towards A, C, literally “towards the parts B, D or towards A, C,” epi ta B, D merê ê epi ta A G.
23. straight lines produced indefinitely from angles less than two right angles, ai de ap: elassonôn ê duo orthôn ekballomenai eis apeipon sumpiptousin, a variation from the more explicit language of Postulate 5. A good deal is left to be understood, namely that the straight lines begin from points at which they meet a transversal, and make with it internal angles on the same side the sum of which is less than two right angles.
26. because they are by hypothesis parallel, literally “because they are supposed parallel,” dia to parallêlous autas hupokeisthai.
56 The usual conclusion in general terms (“Therefore etc.”) repeating the enunciation is, curiously enough, wanting at the end of this proposition.
1. joining...(at the extremities which are) in the same directions (respectively). I have for clearness' sake inserted the words in brackets though they are not in the original Greek, which has “joining...in the same directions” or “on the same sides,” epi ta auta merê epizeugnuousai. The expression “tiwards the same parts,” though usage has sanctioned it, is perhaps not quite satisfactory.
15. DC, CB and 18. DCB. The Greek has “ BC, CD” and “BCD” in these places respectively. Euclid is not always careful to write in corresponding order the letters denoting corresponding points in congruent figures. On the contrary, he evidently prefers the alphabetical order, and seems to disdain to alter it for the sake of beginners or others who might be confused by it. In the case of angles alteration is perhaps unnecessary; but in the case of triangles and pairs of corresponding sides I have ventured to alter the order to that which the mathematician of to-day expects.
59 It is to be observed that, when parallelograms have to be mentioned for the first time, Euclid calls them “parallelogrammic areas” or, more exactly, “parallelogram” areas (parallêlogramma chôria). The meaning is simply areas bounded by parallel straight lines with the further limitation placed upon the term by Euclid that only four-sided figures are so called, although of course there are certain regular polygons which have opposite sides parallel, and which therefore might be said to be areas bounded by parallel straight lines. We gather from Proclus (p. 393) that the word “parallelogram” was first introduced by Euclid, that its use was suggested by I. 33, and that the formation of the word parallêlogrammos (parallel-lined) was analogous to that of euthugrammos (straight-lined or rectilineal).
17, 18, 40. DCB and 36. DC, CB. The Greek has in these places “BCD” and “CD, BC” respectively. Cf. note on I. 33, lines 15, 18.
21. FDC. The text has “DFC.”
22. Let DGE be subtracted. Euclid speaks of the triangle DGE without any explanation that, in the case which he takes (where AD, EF have no point in common), BE, CD must meet at a point G between the two parallels. He allows this to appear from the figure simply.
63 Here and in the next proposition Heiberg brackets the words “But the halves of equal things are equal to one another” on the ground that, since the Common Notion which asserted this fact was interpolated at a very early date (before the time of Theon), it is probable that the words here were interpolated at the same time. Cf. note above (p. 224) on the interpolated Common Notion.
64 [I say that they are also in the same parallels.] Heiberg has proved (Hermes, XXXVIII., 1903, p. 50) from a recently discovered papyrus-fragment (Fay?m towns and their papyri, p. 96, No. IX.) that these words are an interpolation by some one who did not observe that the words “And let AD be joined” are part of the setting-out (ekthesis), but took them as belonging to the construction (kataskeuê) and consequently thought that a diorismos or “definition” (of the thing to be proved) should precede. The interpolator then altered “And” into “For” in the next sentence.
65 complements, paraplêrômata, the figures put in to fill up (interstices).
4. and about AC.... Euclid's phraseology here and in the next proposition implies that the complements as well as the other parallelograms are “about” the diagonal. The words are here peri de tên AG parallêlogramma men estô ta ETh, ZÊ, ta de legomena paraplêrômata ta BK, KD. The expression “the so-called complements” indicates that this technical use of paraplêrômata was not new, though it might not be universally known.
14. since the straight line HF falls.... The verb is in the aorist (enepesen) here and in similar expressions in the following propositions.
2, 3, 6, 45, 48. rectilineal figure, in the Greek “rectilineal” simply, without “figure,” euthugrammon being here used as a substantive, like the similarly formed parallêlogrammon.
1, 3, 30 Proclus (p. 423, 18 sqq.) notes the difference between the word construct (susthêsasthai) applied by Euclid to the construction of a triangle (and, he might have added, of an angle) and the words describe on (anagraphein apo) used of drawing a square on a given straight line as one side. The triangle (or angle) is, so to say, pieced together, while the describing of a square on a given straight line is the making of a figure “from” one side, and corresponds to the multiplication of the number representing the side by itself.
1. the square on , to apo...tetrhagônon, the word anagraphen or anagegrammenon being understood.
71 subtending the right angle. Here hupoteinousês, “subtending,” is used with the simple accusative (tên orthên gônian) instead of being followed by hupo and the accusative, which seems to be the original and more orthodox construction. Cf. I. 18, note.
33. the two sides AB, BD.... Euclid actually writes “DB, BA,” and therefore the equal sides in the two triangles are not mentioned in corresponding order, though he adheres to the words hekatera hekatera “respectively.” Here DB is equal to BC and BA to FB.
73 [But the doubles of equals are equal to one another.] Heiberg brackets these words as an interpolation, since it quotes a Common Notion which is itself interpolated. Cf. notes on I. 37, p. 332, and on interpolated Common Notions, pp. 223-4.
Continue on to Book Two
Return to the Table of Contents
Return to List of Authors and Books