|
Self-organization theory outlines
a process by which any "system"--from atoms to galactic clusters, with
biological life included along the way--takes its characteristic form not
through a complex array of controls imposed from outside the system, but
through a relatively small number of principles of self-guidance operating
within the system.
These basic principles or key patterns
describe the system's fundamental identity--at all levels of its being--within
its broader ecosystem. These principles or patterns of fundamental
identity operate at the level of its smallest constituent parts--to its
overall frame or structure of being, its "outer" shape. These key
patterns are amazingly the same at whatever level we examine the system.
These patterns remain present in
the system even though the system may undergo very dramatic breakdown or
destruction in challenges to its existence coming from its ecosystem.
Because these patterns are still present in the remnants of the system
which survive such crises, they permit the system to rebuild itself, in
accommodation to the ecological changes. Though in many ways the
system has been seriously reworked, it is still very much the same system.
It has not lost its essential identity in the crisis.
Edward N. Lorenz
Meteorologist at the Massachussetts
Institute of Technology.
Lorenz was the individual who elaborated
the "butterfly effect": the tiny turbulence set up by the flapping
of the wings of a small a butterfly in China can stir a larger reaction
in the surrounding air, which can in turn effect the local cloud structuring,
which in turn can set off atmospheric conditions which set up storms that
reach across the Pacific, producing hurricanes of massive violence.
If such small change in the "initial
conditions" can produce such radical impacts on overall weather conditions,
how could we possibly create a weather model that included
all such
possibile sources of influence? In other words, how can we become
scientifically predictive?
Clearly the reductionist system of
knowledge or "science" that we have built our truths on can not work in
such instances. It breaks down in the face of such
chaos.
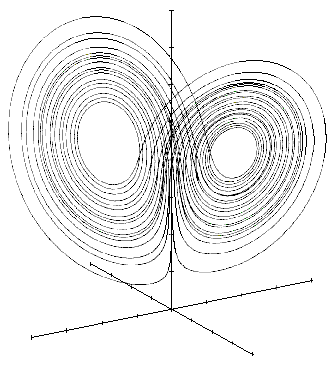
Yet
he also detected intricate patterns in the midst of this chaos; not mathematically
predictable patterns, but patterns that were not random either. In
other words, there was order even in the midst of chaos.
This order was not immediately self-evident.
Yet for those willing to dig into chaos itself (where scientific experimenters
usually left off because their experiments were judged to have "failed")
order was always there to be found.
This order intrigued him. He
thus set out to describe this order.
He noticed about this order-within-chaos
that while events did not repeat themselves exactly, they came close, close
enough that in plotting the movement of these events over time a most definite
pattern
of action resulted. It was not a linear pattern in the sense that
it could be plotted as a single curve on a "scientific" time-series graph.
But a line of movement of events amidst chaos could be plotted on an intriguing
"non-linear" three-dimensional graph.
He also noticed that in plotting
this order-within-chaos, abrupt reversals
in the direction or flow
of events occurred regularly. In other words, the movement of events
through this chaos turned back on itself to suddenly move in the opposite
direction. But it did it in such a way that this movement represented
a definite symmetry of sorts, not perfect, but certainly approaching
symmetry. What interesting order in the midst of chaos!!
 Lorenz'
major works or writings:
"Deterministic Nonperiodic
Flow," Journal of Atmospheric Sciences
(1963)
Stephen Smale
Mathematician
Robert May
Australian mathematician working
in the field of biology at Princeton. In studying the growth in the
equilibrium level of the population of a particular species, he noticed
that this level over time represented a steady linear growth curve when
charted on a time series chart--until it reached a certain level when abruptly
that growth curve would would break down into two lines of movement, one
moving toward ever greater growth, while the other moved toward dramatic
decline--almost symetrically opposite each other in their shapes!
Eventually (though much more quickly
this time) the continuous movement of these two opposing lines of population
growth/decline also abruptly at some point broke down--each into two oposing
lines of movement, so that there were now four lines of growth/decline
describing this population! These four lines in turn would at some
point (again, even more quickly this time) also break down in a doubling
action. As the time between these breakdowns grew ever shorter, the
more chaotic this overall movement appeared. Yet in the small details of
this movement, the overall characteristic pattern persisted--the more difficult
to observe because the details were becoming ever finer and finer.
Thus the seemingly mounting chaos masked in fact a very intricate pattern
of order.
It was chaotic--yet clearly representing
a type of order amidst chaos.
Mitchell Feigenbaum
 Ilya
Prigogine (1917- )
Prigogine received the Nobel Prize
for Chemistry in 1977 for his theory of dissipative structures.
He demonstrated that certain chemical substances possess the ability to
rebuild
themselves in response to disorder or chaos.
This theory might seem to stand in
violation of the Second Law of Thermodynamics which states that all systems
are inevitably prone to entropy--or the loss of their structure
and power (including even the universe itself--which some fell is slowly
running down). But Prigogine demonstrated that though all structures
or systems are indeed subject to the law of entropy--that is, they inevitably
will dissipate their energy and structure in the form of an apparent
aging process of systems "breakdown"--such breakdowns are actually a very
necessary part of the process by which systems adapt their structures
in response to a constantly changing environment. Entropy thus points
not to the collapse or death of a system--but to its on-going adaptation
to life.
All systems have identifiable "boundaries"
that set off the system from its environment--that make it an identifiable
"thing." But these boundaries not only serve to set off
that system from the outside world--but also to connect it to the
ever-evolving complexities of the outside world. These systems
boundaries work in such a way that they give way, "break down" in the face
of that changing environment, in such a way that permits them to let go
of the "old order"--not go down with the ship, so to speak,--but to bounce
back renewed and strengthened in design and action. Thus through
the action of these dissipative structures, new order arises out
of chaos.
Progogine's
major works or writings:
Being to Becoming:
Time and Complexity in the Physical Sciences (1980).
Order Out of Chaos
(1984) (with Isabelle Stengers)
 David
Bohm (1917-1992)
Bohm put forth the view that there
is an "implicate order" that is "folded up" within all reality--even in
the midst of apparent chaos. This inherent urge toward self-order
is very strong--stronger than the seeming "wierdness" or randomness of
quantum behavior. In fact Bohm challenged Bohr strongly in the latter's
view of the essential randomness of life at the quantum level. To
Bohm, order--not randomness--was the foundational instinct of the universe.
Bohm's
major works or writings:
Quantum Theory
(1951)
Causality and Chance in Modern
Physics (1957)
The Special Theory of Relativity
(1966)
Wholeness and the Implicate
Order (1980)
Science, Order and Creativity
(1987)
(with F. David Peat)
On Dialogue
(1990)
Erich Jantsch
All of life works by the principle
of autopoiesis (Greek for "self-production"). Though the living
structure or system undergoes constant change, it retains its recognizable
form or identity--even in the face of extensive self-adaptation.
Jantsch's
major works or writings:
The Self-Organizing
Universe (1980)
Benoit Mandelbrot
In his research work at IBM, Mandelbrot
developed mathematical formulations of these self-replacting patterns
and converted them into actual geometrical designs called "fractals." | 
Richard
Phillips Feynman (1918-1988)
Murray
Gell-Mann (1929- )
Sheldon
L. Glashow (1932- )
Steven
Weinberg (1933- )
Stephen
Hawking (1942- )
Francis
Harry Compton Crick (1916- )
James
Dewey Watson (1928- )
Stephen
Jay Gould
Richard
Dawkins
Jacques
Monod (1910-1976)
Rupert
Sheldrake (1942- )
Deepak
Chopra
Larry
Dossey
Benjamin
Spock (1903-1998)
Noam
Chomsky (1928- )
Daniel
C. Dennett (1942- )
Stanislav
Grof
Ken
Wilber
Joseph
Campbell (1904-1987)
Danah
Zohar
Margaret
J. Wheatley
